Was ist ein Zylinder?
Ein Zylinder ist ein Körper, bei dem zwei gleichartige kreisrunde Grundflächen sich parallel gegenüberstehen und durch einen Mantel miteinander verbunden sind. Ein Zylinder entsteht dadurch, daß man zwei senkrecht übereinanderstehende gleiche Kreise nimmt und jeweils die Kreisränder miteinander verbindet.
Die Grundfläche eines Zylinders ist ein Kreis. 
Jeder Zylinder hat 2 kreisförmige Grundflächen, die zueinander parallel sind. Die gekrümmte Seitenfläche heißt Mantelfläche. Der Abstand der beiden Grundflächen voneinander ist die Höhe des Zylinders. Alle Flächen zusammen bilden die Gesamtoberfläche des Zylinders.
Ein Zylinder ist im einfachsten Fall eine Fläche, deren Punkte von einer festen Gerade, der Achse, denselben Abstand r haben. Da solch eine Fläche unendlich ausgedehnt ist, beschneidet man sie normalerweise mit zwei parallelen Ebenen der Distanz h. Sind die Schnittebenen senkrecht zur Achse, entsteht ein senkrechter (oder gerader) Kreiszylinder mit Radius r und Höhe h.
Die so beschnittene Fläche heißt Mantelfläche des Zylinders. Da man sich einen geraden Kreiszylinder auch durch Rotation einer Strecke um die (parallele) Zylinderachse erzeugt denken kann, wird er auch Drehzylinder genannt. Die erzeugenden Strecken nennt man Mantellinien des Zylinders oder auch Erzeugende. In der Technik versteht man unter einem Zylinder oft den Körper, der von der Mantelfläche und den beiden Schnittkreisflächen eingeschlossen wird. In der Mathematik definiert man einen Zylinder allgemeiner.
Welche Formeln gelten am Zylinder?
Die Gesamtfläche des Zylinderfläche besteht aus zwei Unterbaugruppen und Zylindermantel. Zylinderfläche ist das Produkt aus dem Umfang und die Höhe.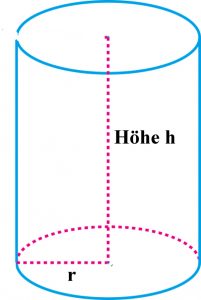 
Es gelten folgende Formeln: Die Grundfläche ist gleich Pi*r², wenn r der Radius ist, und der Umfang der Grundfläche ist gleich 2*Pi*r². Die Mantelfläche hat den Flächeninhalt 2*Pi*r*h, wobei h die Höhe ist. Die Gesamtoberfläche GO ist gleich 2G+M, wobei G die Grundfläche und M die Mantelfläche ist.
Also:
Grundfläche G = Pi * Radius² = π * r²
Mantelfläche M = Umfang * Höhe = (2 * π * r) * h
Gesamtoberfläche GO = 2 * Grundfläche + Mantelfläche
wobei aus einfachem Grund Pi = π = 3,14 ist.
Übungen
1. Ein Folienstift hat eine Höhe von 15,5 cm und einen Umfang von 6 cm. Wie groß ist die Gesamtoberfläche GO dieses Stifts?
Lösung:
Gegeben: h= 15,5 cm
Umfang = 2 * π * r = 6 cm; r = 6/(2 * π) = 0,955 cm
Grundfläche G = 3,14 * 0,955² = 2,86 cm²
Mantelfläche M = Umfang * Höhe = 6 * 15,5 = 93 cm²
Gesamtoberfläche GO = 2 * G + M = 98,7 cm²
2. Konservendosen mit einem Durchmesser von 11 cm und einer Höhe von 8,0 cm sollen mit einem Etikett, 
das sich nicht überlappt, beklebt werden. Wie groß ist die zu beklebende Fläche?
Lösung:
Gegeben: d = 11 cm; h = 8,0 cm
Gesucht: Mantelfläche M
Antwort: Mantelfläche M = 2 * Pi * 5,5 * 8 = 276,46 cm²
Es muss bei jeder Dose eine Fläche von etwa 276,46 cm² beklebt werden.
3. Gegeben ist ein Zylinder mit r = 6 cm und h = 18 cm.
Wie groß ist die Gesamtoberfläche (GO) des Zylinders?
Lösung:
Grundfläche G = Pi * Radius² = π * r² = 3,14 * 6² = 113,04
Mantelfläche M = Umfang * Höhe = (2 * π * r) * h = (2 * 3,14 * 6) * 18 = 678,24
Gesamtoberfläche GO = 2 * Grundfläche + Mantelfläche = 2 * 113,04 + 678,24 = 904,32
Die Gesamtoberfläche des Zylinders (GO) ist 904,32 cm².
Quelle:
http://www.mathepower.com
https://de.wikipedia.org/wiki
http://www.aufgabenfuchs.de
http://fontaneum.de